
Innhold
For at to former skal være kongruente, må hver ha samme antall sider, og deres vinkler må også være de samme. De enkleste måtene å bestemme om to former er sammenfallende, er å rotere en av formene til den er stilt opp med den andre, eller bare stable formene oppå hverandre for å se om noen ender stikker ut. Hvis du ikke er i stand til å bevege formene fysisk, kan du bruke formler for å bestemme om formene er kongruente.
Congruent Circles
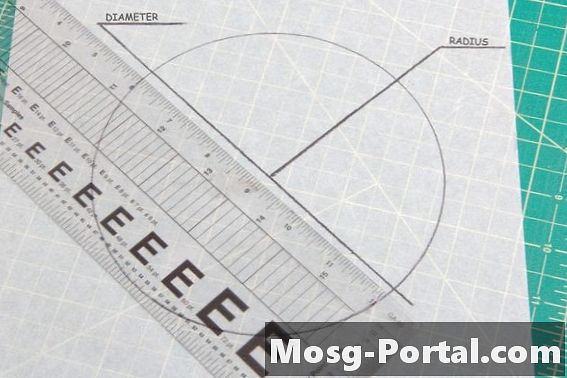
••• Ray Robert Green / Demand MediaAlle sirkler har samme vinkel på 360 grader. Den eneste faktoren for å bestemme kongruensen av to sirkler er å sammenligne størrelsen. Diameteren er en rett linje gjennom sentrum av sirkelen fra kant til kant, mens radiusen til en sirkel er lengden fra midten til den ytre kanten. Å måle en av disse på begge kretser vil bevise om de er kongruente.
parallellogrammer
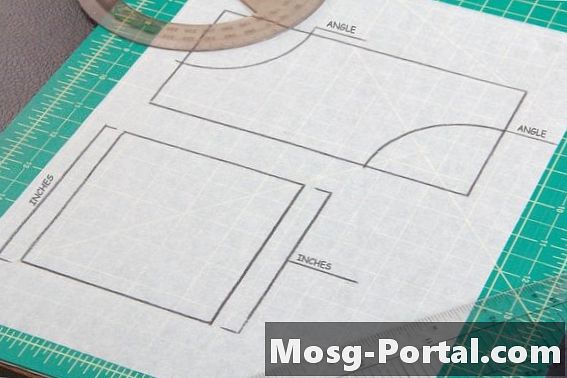
Et parallellogram har to par parallelle sider, for eksempel firkanter og rektangler. De motsatte sidene eller vinklene til et parallellogram har samme mål, så det er nødvendig å ta to vinkel- eller sidemålinger på et parallellogram, en fra hvert sidepar, for å sammenligne kongruens med en annen form.
Triangles
••• Ray Robert Green / Demand MediaFor å finne sammenhengen mellom trekanter må du bestemme størrelsen på hver vinkel eller side, siden alle tre kan være forskjellige. Det er tre postulater som kan brukes til å identifisere kongruente trekanter. SSS-postulatet er når du måler alle tre sidene i hver trekant. ASA-postulatet sier at hvis to vinkler og deres sammenkoblende side stemmer overens med den i den andre trekanten, er de kongruente. SAS-postulatet gjør det motsatte, og måler to sider og deres koblingsvinkel for å sammenligne med den andre trekanten.
Teoremer for Congruent Triangles

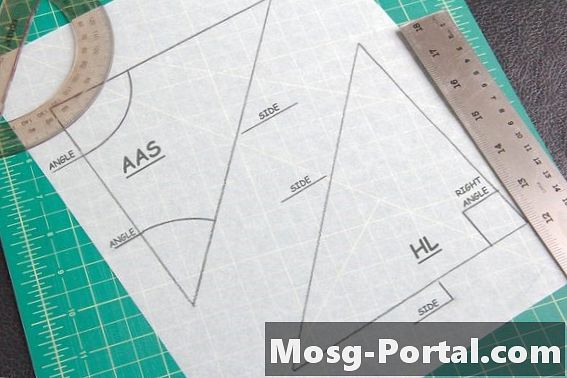
To teoremer er nyttige for å finne kongruente trekanter. AAS-teoremet sier at hvis to vinkler og en side som ikke forbinder de to er lik den for en annen trekant, så er de kongruente. Hypotenuse-Leg-teoremet gjelder bare trekanter med en 90-graders eller "riktig" vinkel. Dette er når du måler hypotenusen - siden motsatt av 90 graders vinkel - og en av de andre sidene av trekanten, for å sammenligne med den andre formen.