Laws of Pendulum Motion

Innhold

• TL; DR (for lang; ikke lest)
• Enkel harmonisk bevegelse
• Laws of a Simple Pendulum
• Enkel pendul derivasjon
• Faktorer som påvirker pendelbevegelsen
• Lengde på pendeleksempel
• Enkel pendeldefinisjon
• Newtons lover i pendler

Pendler har interessante egenskaper som fysikere bruker for å beskrive andre objekter. For eksempel følger planetbane et lignende mønster, og å svinge på et svingsett kan føles som om du er på en pendel. Disse egenskapene kommer fra en rekke lover som styrer pendelens bevegelse. Ved å lære disse lovene, kan du begynne å forstå noen av de grunnleggende grunnleggende tingene for fysikk og bevegelse generelt.

TL; DR (for lang; ikke lest)

Bevegelsen til en pendel kan beskrives ved å bruke θ (t) = θ_maxcos (2πt / T) der θ representerer vinkelen mellom strengen og den vertikale linjen midt i midten, t representerer tid, og T er perioden, den tiden som er nødvendig for at en fullstendig syklus av pendelbevegelsen skal skje (målt med 1 / f), av bevegelsen for en pendel.

Enkel harmonisk bevegelse

Enkel harmonisk bevegelse, eller bevegelse som beskriver hvordan en gjenstandshastighet svinger proporsjonalt med mengden forskyvning fra likevekt, kan brukes til å beskrive ligningen til en pendel. En pendul bob svingende holdes i bevegelse av denne kraften som virker på den når den beveger seg frem og tilbake.

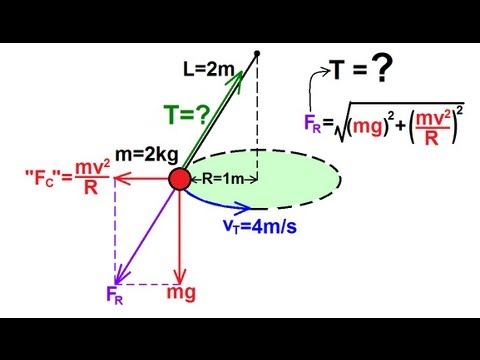
••• Syed Hussain Ather

Lovene som styrer pendelbevegelse førte til oppdagelsen av en viktig eiendom. Fysikere bryter opp krefter til en vertikal og en horisontal komponent. I pendelbevegelse, tre krefter jobber direkte på pendelen: massen til boben, tyngdekraften og spenningen i strengen. Masse og tyngdekraft fungerer begge vertikalt nedover. Siden pendelen ikke beveger seg opp eller ned, kansellerer den vertikale komponenten i strengspenningen massen og tyngdekraften.

Dette viser at massen til en pendel ikke har noen relevans for bevegelsen, men den horisontale strengspenningen gjør det. Enkel harmonisk bevegelse ligner sirkulær bevegelse. Du kan beskrive et objekt som beveger seg i en sirkulær bane som vist på figuren over ved å bestemme vinkelen og radius den tar i den tilsvarende sirkulære banen. Deretter kan du finne ligninger ved å bruke trigonometrien til høyre trekant mellom sirkelsenteret, gjenstandenes plassering og forskyvningen i begge retninger x og y x = rsin (θ) og y = rcos (θ).

Den endimensjonale ligningen til et objekt i enkel harmonisk bevegelse er gitt av x = r cos (ωt). Du kan erstatte videre EN til r der EN er den amplitude, maksimal forskyvning fra gjenstandens startposisjon.

Vinkelhastigheten ω med hensyn til tid t for disse vinklene θ er gitt av θ = ωt. Hvis du erstatter ligningen som knytter vinkelhastigheten til frekvensen f, ω = 2πf_, kan du forestille deg denne sirkulære bevegelsen, da, som en del av en pendel som svinger frem og tilbake, så er den resulterende enkle harmoniske bevegelsesligningen _x = A cos (2πft).

Laws of a Simple Pendulum

••• Syed Hussain Ather

Pendler, som masser på en fjær, er eksempler på enkle harmoniske oscillatorer: Det er en gjenopprettende kraft som øker avhengig av hvor fortrengt pendelen er, og bevegelsen deres kan beskrives ved å bruke enkel harmonisk oscillatorligning θ (t) = θ_maxcos (2πt / T) der θ representerer vinkelen mellom strengen og den vertikale linjen midt i midten, t representerer tid og T er den periode, den tiden som er nødvendig for at en fullstendig syklus av pendelbevegelsen skal skje (målt med 1 / f), av bevegelsen for en pendel.

θ_max er en annen måte å definere det maksimale vinkelen svinger under pendelens bevegelse og er en annen måte å definere pendelens amplitude. Dette trinnet blir forklart nedenfor under avsnittet "Enkel pendeldefinisjon."

En annen implikasjon av lovene til en enkel pendel er at svingningsperioden med konstant lengde er uavhengig av objektets størrelse, form, masse og materiale på enden av strengen. Dette vises tydelig gjennom den enkle pendulderivasjonen og ligningene som resulterer.

Enkel pendul derivasjon

Du kan bestemme ligningen for a enkel pendel, definisjonen som avhenger av en enkel harmonisk oscillator, fra en serie trinn som begynner med ligningsbevegelsen for en pendel. Fordi tyngdekraften til en pendel tilsvarer kraften i pendelbevegelsen, kan du stille dem like til hverandre ved å bruke Newtons andre lov med en pendelmasse M, strenglengde L, vinkel θ, gravitasjonsakselerasjon g og tidsintervall t.

••• Syed Hussain Ather

Du setter Newtons andre lov som tilsvarer treghetsøyeblikket I = mr²_for litt masse _m og radius for den sirkulære bevegelsen (lengden på strengen i dette tilfellet) r ganger vinkelakselerasjonen α.

Det er andre måter å lage en enkel pendulderivasjon på. Forstå betydningen bak hvert trinn for å se hvordan de er relatert. Du kan beskrive en enkel pendelbevegelse ved å bruke disse teoriene, men du bør også ta hensyn til andre faktorer som kan påvirke enkel pendelteori.

Faktorer som påvirker pendelbevegelsen

Hvis du sammenligner resultatet av denne avledningen θ (t) = θ_maxcos (t (L / g)²) til ligningen til en enkel harmonisk oscillator (_θ (t) = θ_maxcos (2πt / T)) b_y hvis du setter dem lik hverandre, kan du utlede en ligning for perioden T.

Legg merke til at denne ligningen T = 2π (L / g)^-1/2 avhenger ikke av massen M av pendelen, amplituden θ_max, heller ikke på tiden t. Det betyr at perioden er uavhengig av masse, amplitude og tid, men i stedet er avhengig av lengden på strengen. Det gir deg en kortfattet måte å uttrykke pendelbevegelse på.

Lengde på pendeleksempel

Med ligningen i en periode T = 2π (L / g) __^-1/2, kan du omorganisere ligningen for å oppnå L = (T / 2_π)² / g_ og erstatter 1 sek for T og 9,8 m / s² til g for å oppnå L = 0,0025 moh. Husk at disse likningene av enkel pendelteori antar at lengden på strengen er friksjonsfri og masseløs. For å ta hensyn til disse faktorene vil det kreve mer kompliserte ligninger.

Enkel pendeldefinisjon

Du kan trekke pendelen bakvinkelen θ å la den svinge fram og tilbake for å se den svinge akkurat som en fjær kan. For en enkel pendel kan du beskrive det ved å bruke bevegelsesligninger for en enkel harmonisk oscillator. Bevegelsesligningen fungerer bra for mindre verdier av vinkel og amplitude, den maksimale vinkelen, fordi den enkle pendelmodellen er avhengig av tilnærmingen som sin (θ) ≈ θ for en viss pendulvinkel θ. Når verdiene vinkler og amplituder blir større enn omtrent 20 grader, fungerer ikke denne tilnærmingen også.

Prøv det selv. En pendel som svinger med en stor begynnelsesvinkel θ vil ikke svinge like regelmessig for å tillate deg å bruke en enkel harmonisk oscillator for å beskrive det. I en mindre startvinkel θ, pendelen nærmer seg en regelmessig, oscillerende bevegelse mye lettere. Fordi massen av en pendel ikke har noen betydning for bevegelsen, har fysikere bevist at alle pendler har samme periode for svingningsvinkler - vinkelen mellom midten av pendelen på det høyeste punktet og sentrum av pendelen i sin stoppede stilling - mindre enn 20 grader.

For alle praktiske formål med en pendel som er i bevegelse, vil pendelen til slutt avta og komme til å stoppe på grunn av friksjonen mellom strengen og dens festede punkt over så vel som på grunn av luftmotstand mellom pendelen og luften rundt den.

For praktiske eksempler på pendelbevegelse, vil perioden og hastigheten avhenge av hvilken type materiale som ble brukt som ville forårsake disse eksemplene på friksjon og luftmotstand. Hvis du utfører beregninger på teoretisk pendul oscillerende atferd uten å gjøre rede for disse kreftene, vil den stå for en pendel som svinger uendelig.

Newtons lover i pendler

Newtons første lov definerer gjenstandenes hastighet som svar på krefter. Loven sier at hvis en gjenstand beveger seg med en bestemt hastighet og i en rett linje, vil den fortsette å bevege seg med den hastigheten og i en rett linje, uendelig, så lenge ingen annen kraft virker på den. Se for deg å kaste en ball rett frem - ballen ville gå rundt jorden igjen og igjen hvis luftmotstand og tyngdekraft ikke virket på den. Denne loven viser at siden en pendel beveger seg side om side og ikke opp og ned, har den ingen opp og ned krefter som virker på den.

Newtons andre lov brukes til å bestemme nettokraften på pendelen ved å sette gravitasjonskraften lik kraften til strengen som trekker tilbake opp på pendelen. Hvis du setter disse ligningene lik hverandre, kan du utlede bevegelsesligningene for pendelen.

Newtons tredje lov sier at hver handling har en reaksjon av lik kraft. Denne loven fungerer med den første loven som viser at selv om massen og tyngdekraften avbryter den vertikale komponenten i strengspenningsvektoren, er det ingenting som avbryter den horisontale komponenten. Denne loven viser at kreftene som virker på en pendel kan kansellere hverandre.

Fysikere bruker Newtons første, andre og tredje lov for å bevise den horisontale strengspenningen beveger pendelen uten hensyn til masse eller tyngdekraft. Lovene i en enkel pendel følger ideene til Newtons tre bevegelseslover.