Innhold
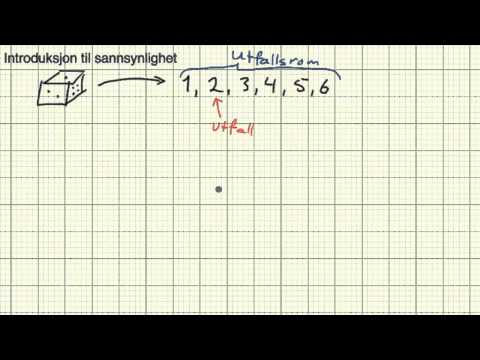
Sannsynlighet måler sannsynligheten for at en hendelse inntreffer. Matematisk uttrykt, tilsvarer sannsynligheten antallet måter en spesifisert hendelse kan oppstå, delt på det totale antallet av alle mulige hendelsesforekomster. For eksempel, hvis du har en pose som inneholder tre klinkekuler - en blå marmor og to grønne klinkekuler, er sannsynligheten for å gripe et usynlig blått marmorsyn 1/3. Det er ett mulig utfall der den blå marmoren er valgt, men tre totale mulige prøveutfall - blå, grønn og grønn. Ved å bruke samme matematikk er sannsynligheten for å gripe en grønn marmor 2/3.
Lov om store tall
Du kan oppdage den ukjente sannsynligheten for en hendelse gjennom eksperimentering. Ved å bruke forrige eksempel kan du si at du ikke vet sannsynligheten for å tegne en viss farget marmor, men du vet at det er tre kuler i vesken. Du utfører en prøve og tegner en grønn marmor. Du utfører en ny prøve og tegner en ny grønn marmor. På dette tidspunktet kan du hevde at vesken bare inneholder grønne klinkekuler, men basert på to forsøk er forutsigelsen din ikke pålitelig. Det er mulig posen bare inneholder grønne klinkekuler, eller det kan være de to andre er røde, og du valgte den eneste grønne marmoren i rekkefølge. Hvis du utfører den samme prøven 100 ganger, vil du sannsynligvis oppdage at du velger en grønn marmor rundt 66% prosent av tiden. Denne frekvensen speiler riktig sannsynlighet mer nøyaktig enn det første eksperimentet. Dette er loven om store tall: jo større antall forsøk, jo mer nøyaktig vil hyppigheten av et hendelsesresultat gjenspeile dens faktiske sannsynlighet.
Lov om subtraksjon
Sannsynlighet kan bare variere fra verdier 0 til 1. En sannsynlighet på 0 betyr at det ikke er noen mulige utfall for den hendelsen. I vårt forrige eksempel er sannsynligheten for å tegne en rød marmor null. En sannsynlighet på 1 betyr at hendelsen vil oppstå i hver prøve. Sannsynligheten for å tegne enten en grønn marmor eller en blå marmor er 1. Det er ingen andre mulige utfall. I posen som inneholder en blå marmor og to grønne, er sannsynligheten for å tegne en grønn marmor 2/3. Dette er et akseptabelt antall fordi 2/3 er større enn 0, men mindre enn 1 - innenfor området for akseptable sannsynlighetsverdier. Når du vet dette, kan du bruke loven om subtraksjon, som sier at hvis du vet sannsynligheten for en hendelse, kan du nøyaktig oppgi sannsynligheten for at den hendelsen ikke skal skje. Når du kjenner til sannsynligheten for å tegne en grønn marmor er 2/3, kan du trekke den verdien fra 1 og riktig bestemme sannsynligheten for ikke å tegne en grønn marmor: 1/3.
Lov om multiplikasjon
Hvis du vil finne sannsynligheten for at to hendelser skal oppstå i sekvensielle studier, bruk loven om multiplikasjon. For eksempel, i stedet for den forrige tre-marmorerte vesken, si at det er en fem-marmorert pose. Det er en blå marmor, to grønne klinkekuler og to gule klinkekuler. Hvis du vil finne sannsynligheten for å tegne en blå marmor og en grønn marmor, i begge rekkefølge (og uten å returnere den første marmoren i posen), finn sannsynligheten for å tegne en blå marmor og sannsynligheten for å tegne en grønn marmor. Sannsynligheten for å trekke en blå marmor fra posen med fem kuler er 1/5. Sannsynligheten for å tegne en grønn marmor fra det gjenværende settet er 2/4, eller 1/2. Å korrekt anvende loven om multiplikasjon innebærer å multiplisere de to sannsynlighetene, 1/5 og 1/2, for en sannsynlighet på 1/10. Dette uttrykker sannsynligheten for at de to hendelsene skal oppstå sammen.
Tilleggsloven
Ved å bruke det du vet om multiplikasjonsloven, kan du bestemme sannsynligheten for at bare en av to hendelser skal oppstå. Tilleggsloven sier at sannsynligheten for at en av to hendelser skal være lik summen av sannsynlighetene for hver hendelse som skal skje hver for seg, minus sannsynligheten for at begge hendelser inntreffer. I den fem-marmorerte posen, si at du vil vite sannsynligheten for å tegne enten en blå marmor eller en grønn marmor. Legg sannsynligheten for å tegne en blå marmor (1/5) til sannsynligheten for å tegne en grønn marmor (2/5). Summen er 3/5. I det forrige eksemplet som uttrykker multiplikasjonsloven, fant vi sannsynligheten for å tegne både en blå og grønn marmor er 1/10. Trekk dette fra summen av 3/5 (eller 6/10 for lettere subtraksjon) for en endelig sannsynlighet på 1/2.