Innhold
- Motivasjon
- Uttalelse av teorem
- Hvorfor det er overalt
- Gaussian Copulas
- derivasjon
- Computational Convenience
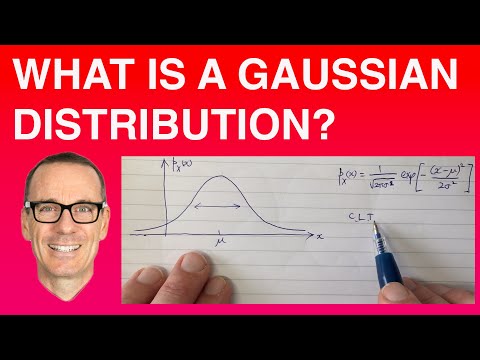
I statistikk brukes den Gaussiske eller normale distribusjonen for å karakterisere komplekse systemer med mange faktorer. Som beskrevet i Stephen Stiglers Historie om statistikk, oppfant Abraham De Moivre distribusjonen som bærer Karl Fredrick Gauss navn. Gauss 'bidrag lå i anvendelsen av distribusjonen til de minste rutene tilnærming for å minimere feil ved å montere data med en linje som passer best. Han gjorde det dermed til den viktigste feilfordelingen i statistikk.
Motivasjon
Hva er fordelingen av et utvalg data? Hva om du ikke vet hvilken underliggende distribusjon? Er det noen måte å teste hypoteser om dataene uten å vite den underliggende fordelingen? Takket være Central Limit Theorem er svaret ja.
Uttalelse av teorem
Den oppgir at et utvalgsmiddel fra en uendelig populasjon er tilnærmet normalt, eller Gauss, med gjennomsnitt det samme som den underliggende populasjonen, og varians som er lik populasjonsvariansen delt på utvalgsstørrelsen. Tilnærmingen forbedres ettersom prøvestørrelsen blir stor.
Tilnærmelsesuttalelsen er noen ganger feilaktig som en konklusjon om konvergens til en normal fordeling. Siden den omtrentlige normalfordelingen endres når prøvestørrelsen øker, er en slik uttalelse misvisende.
Teoremet ble utviklet av Pierre Simon Laplace.
Hvorfor det er overalt
Normale fordelinger er allestedsnærværende. Årsaken kommer fra Central Limit Theorem. Ofte, når en verdi måles, er det sumeffekten av mange uavhengige variabler. Derfor har verdien som måles i seg selv en prøve-middelkvalitet for den. For eksempel kan en fordeling av utøverens prestasjoner ha en bjelleform, som et resultat av forskjeller i kosthold, trening, genetikk, coaching og psykologi. Selv herrehøyder har en normal fordeling, og er en funksjon av mange biologiske faktorer.
Gaussian Copulas
Det som kalles en "copula-funksjon" med en Gauss-distribusjon, var i nyhetene i 2009 på grunn av bruken til å vurdere risikoen for å investere i sikkerhetsstillte obligasjoner. Misbruk av funksjonen var medvirkende i finanskrisen 2008-2009. Selv om det var mange årsaker til krisen, burde Gauss-distribusjoner i ettertid ikke ha blitt brukt. En funksjon med tykkere hale ville gitt større sannsynlighet for uønskede hendelser.
derivasjon
Den sentrale begrensningsteoremet kan påvises i mange linjer ved å analysere øyeblikkegenererende funksjon (mgf) av (utvalgsmengde - populasjonsmiddel) /? (Populasjonsvarians / prøvestørrelse) som en funksjon av mgf av den underliggende populasjonen. Tilnærmelsesdelen av teoremet introduseres ved å utvide den underliggende befolkningens mgf som en kraftserie, og viser at de fleste begrepene er ubetydelige ettersom utvalgsstørrelsen blir stor.
Det kan påvises i langt færre linjer ved å bruke en Taylor-utvidelse på den karakteristiske ligningen for samme funksjon og gjøre prøvestørrelsen stor.
Computational Convenience
Noen statistiske modeller antar at feilene er gaussiske. Dette gjør det mulig å bruke fordelinger av funksjoner av normale variabler, som chi-square- og F-distribusjon, i hypotesetesting. Spesielt i F-testen er F-statistikken sammensatt av et forhold mellom chi-kvadratfordelinger, som i seg selv er funksjoner for en normal variansparameter. Forholdet mellom de to fører til at avviken avbryter, noe som muliggjør test av hypotese uten kunnskap om avvikene bortsett fra deres normalitet og konstanthet.