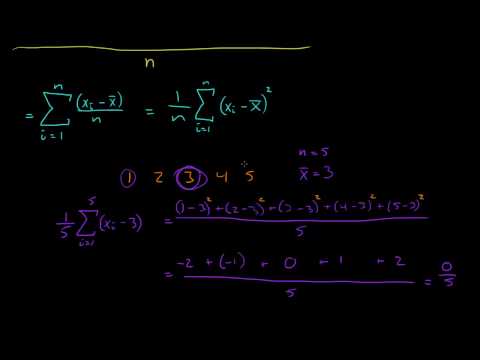
Innhold
Evnen til å beregne gjennomsnittet eller middelverdien til en gruppe tall er viktig i alle aspekter av livet. Hvis du er en professor som tildeler bokstavkarakterer til eksamenspoeng og tradisjonelt gir en karakter på B- til en midt-i-pakken, må du tydeligvis vite hvordan midten av pakken ser ut numerisk. Du trenger også en måte å identifisere poengsummer som outliers, slik at du kan bestemme når noen fortjener en A eller A + (utenom perfekte score, åpenbart), samt hva som fortjener en sviktende karakter.
Av denne og relaterte grunner inkluderer komplette data om gjennomsnitt gjennomsnittlig informasjon om hvor tett gruppert rundt gjennomsnittlig poengsum score generelt. Denne informasjonen formidles ved hjelp av standardavvik og, relatert, den varians av en statistisk prøve.
Målinger av variasjon
Du har nesten helt sikkert hørt eller sett begrepet "gjennomsnittlig" brukt i referanse til et sett med tall eller datapunkter, og du har sannsynligvis en ide om hva det oversettes til i det daglige språket. Hvis du for eksempel leser at gjennomsnittshøyden til en amerikansk kvinne er omtrent 5 4 ", konkluderer du med en gang at" gjennomsnittlig "betyr" typisk ", og at omtrent halvparten av kvinnene i USA er høyere enn dette mens omtrent halvparten er kortere.
Matematisk er gjennomsnitt og gjennomsnitt nøyaktig det samme: Du legger til verdiene i et sett og deler med antall elementer i settet. For eksempel, hvis en gruppe på 25 scorer på et 10 spørsmål spørsmål fra 3 til 10 og legger opp til 196, er gjennomsnittlig (gjennomsnittlig) poengsum 196/25, eller 7,84.
Medianen er midtpunktverdien i et sett, tallet at halvparten av verdiene ligger over og halvparten av verdiene ligger under. Det er vanligvis nær gjennomsnittet (gjennomsnittet), men er ikke det samme.
Variansformel
Hvis du øyeeplet et sett på 25 score som de ovenfor og ser nesten ingenting annet enn verdier på 7, 8 og 9, er det intuitivt fornuftig at gjennomsnittet skal ligge på rundt 8. Men hva om du ser nesten ingenting annet enn score på 6 og 10 ? Eller fem score på 0 og 20 score på 9 eller 10? Alle disse kan gi samme gjennomsnitt.
Varians er et mål på hvor vidt punktene i et datasett er spredt om gjennomsnittet. For å beregne varians for hånd, tar du den aritmetiske forskjellen mellom hvert av datapunktene og gjennomsnittet, kvadrerer dem, legger til summen av rutene og deler resultatet med ett mindre enn antall datapunkter i prøven. Et eksempel på dette er gitt senere. Du kan også bruke programmer som Excel eller nettsteder som Rapid Tables (se Ressurser for flere nettsteder).
Variansen er betegnet med σ2, en gresk "sigma" med en eksponent på 2.
Standardavvik
Standardavviket til en prøve er ganske enkelt kvadratroten til variansen. Årsaken kvadrater brukes når beregning varians er at hvis du bare legger sammen de individuelle forskjellene mellom gjennomsnittet og hvert enkelt datapunkt, er summen alltid null fordi noen av disse forskjellene er positive og noen er negative, og de avbryter hverandre . Å kvadratere hvert begrep eliminerer denne fallgruven.
Eksempel på varians og standardavviksproblem
Anta at du får de 10 datapunktene:
4, 7, 10, 5, 7, 6, 9, 8, 5, 9
Finn gjennomsnittet, variansen og standardavviket.
Først legger du de 10 verdiene sammen og deler med 10 for å få gjennomsnittet (gjennomsnittet):
70/10 = 7.0
For å få variansen, kvadrat forskjellen mellom hvert datapunkt og gjennomsnittet, legg disse sammen og del resultatet med (10 - 1), eller 9:
9 + 0 + 9 + . . . + 4 = 36
σ2= 36/9 = 4.0
Standardavviket σ er bare kvadratroten på 4.0 eller 2.0.