Innhold
Standardfeilen til middelverdien, også kjent som standardavviket for middelverdien, hjelper til med å bestemme forskjellene mellom mer enn ett utvalg av informasjon. Beregningen gjør rede for variasjoner som kan være til stede i dataene. Hvis du for eksempel tar vekten til flere prøver av menn, kan målingene variere vesentlig i hver prøve; noen kan veie 150 pund, mens andre, 300 pund. Imidlertid vil gjennomsnittet av disse prøvene variere med bare noen få kilo. Standardfeilen til middelverdien illustrerer hvor mye de forskjellige vektene varierer fra gjennomsnittet.
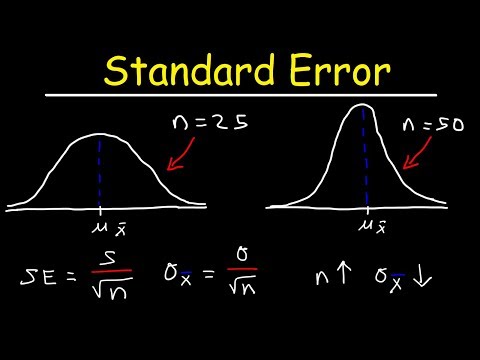
Skriv formelen σM = σ / √N for å bestemme standardfeilen til middelverdien. I denne formelen står σM for standardfeilen til middelverdien, antallet du leter etter, σ står for standardavviket for den opprinnelige distribusjonen og √N er kvadratet til prøvestørrelsen.
Bestem standardavviket for den opprinnelige distribusjonen. Standardavviket forteller oss ganske enkelt hvor langt fra hverandre tallene er på tallinjen. Informasjonen kan gis til deg hvis du arbeider med et statistikkproblem. I så fall bytter du ut σ i formelen din med standardavviket. Hvis det ikke blir gitt, må du finne det på egen hånd.
Finn gjennomsnittet av antall sett hvis standardavviket ikke er gitt; det vil si legge til alle tallene og dele den summen med antall elementer du la til. Trekk gjennomsnittet fra hvert av de opprinnelige tallene dine, og kvadrat resultatet av hvert. Bestem gjennomsnittet av dette nye settet med tall du jobbet ut; svaret vil gi deg variansen. Plasser variansen for å finne standardavviket. Plugg inn nummeret for σ-symbolet i formelen.
Bestem prøvestørrelsen. Prøvestørrelsen er antall elementer eller observasjoner du jobber med. Bytt ut N i formelen med prøvestørrelsen.
Finn kvadratroten til prøvestørrelsen med kalkulatoren.
Del standardavviket med kvadratroten av prøvestørrelsen. Svaret vil gi deg standardfeilen til middelverdien.